1 📑Metadata
摘要
Transformers for graph data are increasingly widely studied and successful in numerous learning tasks. Graph [[inductive biases]] are crucial for Graph Transformers, and previous works incorporate them using message-passing modules and/or positional encodings. However, Graph Transformers that use message-passing inherit known issues of message-passing, and differ significantly from Transformers used in other domains, thus making transfer of research advances more difficult. On the other hand, Graph Transformers without message-passing often perform poorly on smaller datasets, where inductive biases are more important. To bridge this gap, we propose the Graph Inductive bias Transformer (GRIT) — a new Graph Transformer that incorporates graph inductive biases without using message passing. GRIT is based on several architectural changes that are each theoretically and empirically justified, including: learned relative positional encodings initialized with random walk probabilities, a flexible attention mechanism that updates node and node-pair representations, and injection of degree information in each layer. We prove that GRIT is expressive — it can express shortest path distances and various graph propagation matrices. GRIT achieves state-of-the-art empirical performance across a variety of graph datasets, thus showing the power that Graph Transformers without message-passing can deliver.
结论
Observing the performance gap of Graph Transformers between small and large-scale datasets, we argue for the importance of graph inductive biases in Graph Transformers. Motivated by promoting inductive biases in Graph Transformers without message-passing, we propose GRIT, based on three theoretically and empirically motivated design choices for incorporating graph inductive biases. Our learned relative positional encodings initialized with RRWP along with our flexible attention mechanism allow for an expressive model that can provably capture shortest path distances and general families of graph propagations. Theoretical results show that the RRWP initialization is strictly more expressive than shortest path distances when used in the GD-WL graph isomorphism test (Zhang et al., 2023), and a synthetic experiment shows that our flexible attention mechanism is indeed able to learn graph propagation matrices that other Graph Transformers are not as capable of learning. Our GRIT model achieves state-of-the-art performance across a wide range of graph datasets, showing that data complexity can be improved for Graph Transformers without integrating local message-passing modules. Nonetheless, GRIT is not the final chapter for graph inductive biases in Transformers; future work can address limitations of our work, such as GRIT'sscaling for updating pair representations, and lack of upper bounds on expressive power.
2 💡Note
2.1 论文试图解决什么问题?
- Graph inductive biases in graph transformer.
- Graph Transformers that use message-passing inherit known issues of message-passing, and differ significantly from Transformers used in other domains。
- Graph Transformers without message-passing often perform poorly on smaller datasets, where inductive biases are more important.
2.2 这是否是一个新的问题?
Yes, the problem of graph inductive biases in graph transformers has not been explored previously.
2.3 这篇文章要验证一个什么科学假设?
The proposed Graph Inductive bias Transformer (GRIT), a new Graph Transformer that incorporates graph inductive biases without using message passing, bridges the performance gap in which message-passing-based methods do not perform as well in large datasets, and non-message-passing Transformers do not perform as well in small datasets.
2.4 有哪些相关研究?如何归类?谁是这一课题在领域内值得关注的研究员?
2.4.1 Transformers for Euclidean Domains
- Suffer from a lack of inductive bias compared to RNNs and CNNs.
- Require a large amount of training data to perform well.
2.4.2 Positional Encoding and Structural Encoding for Graphs
- Positional Encoding (PE) & Structural Encoding (SE)
- To enhance both MPNNs and Graph Transformers
- To capture various types of graph features
- Shortest-path distances
- Identity-awareness
- Spectral information
- To capture various types of graph features
- Note: PE and SE are used interchangeably.
2.4.3 Graph Transformers with Message-Passing
- Transformer with Laplacian Positional Encoding (LapPE).
- SAN
- Use both sparse and global attention mechanism at each layer.
- Introduce an extra transformer to encode LapPE.
- SignNet
- Specialized symmetry-invariant encoder for LapPE.
- Use message-passing modules to process Laplacian eigenvectors.
- RWSE
- Use random walk structural encodings.
- Integrate message-passing modules.
2.4.4 Graph Transformers without Message-Passing
- Use relative positional encodings for each pair of nodes.
- SPDPE
- Shortest-path distance positional encodings.
- Generalized-Distance Transformers
- Resistance distances.
- Perform well on large datasets but worse on smaller ones, compared
to hybrid Graph Transformers and MPNNs.
- Due to the lack of sufficient inductive bias, they are not as capable in enabling attention mechanisms to perform local message-passing when necessary.
- SPDPE
- TokenGT
- View both nodes and edges as tokens, and uses LapPE or orthogonal random features.
- Relational Transformer
- Update both node and edge tokens.
- EGT
- Use SVD-based PE instead of LapPE for directed graphs.
- Introduce PE based on heat kernels and other graph kernels.
2.5 🔴论文中提到的解决方案之关键是什么?
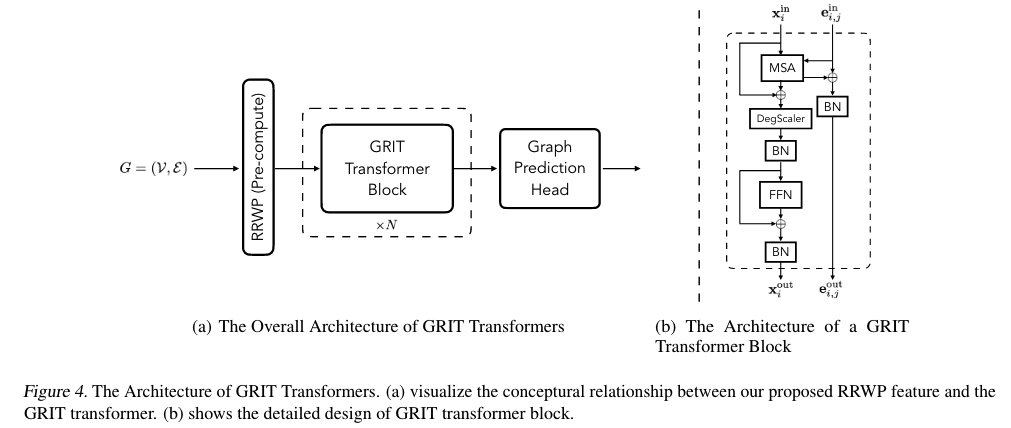
2.5.1 Learned Random Walk Relative Encodings
- As the message-passing module is removed, the positional encoding must adequately capture the graph structure.
- RRWP: Relative Random
Walk Probabilities initial positional
encoding
is the probability that i hops to j in one step of a simple random walk. is the identity matrix - Diagonal
can additionally be utilized as an initial node-level structural encoding --> Random Walk Structural Encodings (RWSE) controls the maximum length of random walks considered.
can be updated by an element-wise to get new relative positional encodings - Expressive power
- Providing a useful inductive bias
2.5.2 Flexible Attention Mechanism with Absolute and Relative Representations
- Most current designs of the self-attention mechanism are based on node-token-level PE and node-token-level representations, but this does not fully capture the relative positional information between pairs of nodes.
- In each transformer layer, node representations
and node-pair representations are both updated: - Initialize these using the initial node features and RRWP positional
encodings.
. . - Set
if there is no observed edge from i to j in the original graph.
- Compute the attention score.
is a non-linear activation (ReLU by default) and are learnable weight matrices; indicates elementwise multiplication; is the signed-square-root, which stabilizes training by reducing the magnitude of large inputs.
- Can be extended to multiple heads (say,
heads) by assigning different weight matrices for different heads.
- Initialize these using the initial node features and RRWP positional
encodings.
2.5.3 Injecting Degree Information
- Attention mechanisms are innately invariant to node degrees, analogously to mean-aggregation; this introduces extra ambiguities and hence reduces expressive power in processing graph-structured data.
- Inject degree information into the node representations:
is the degree of node , and are learnable weights. - Follow this with a standard feed-forward network (FFN) to update the node representations.
- Apply batch normalization instead of the standard layer normalization
2.6 论文中的实验是如何设计的?
- 5 benchmarks from the Benchmarking GNNs work.
- 2 benchmarks from the recently developed Long-Range Graph Benchmark.
- Larger datasets ZINC-full (∼ 250,000 graphs) graphs and PCQM4Mv2 (∼ 3,700,000 graphs)
2.7 用于定量评估的数据集是什么?评估标准是什么?Baseline 是什么?
2.7.1 Benchmarking GRIT
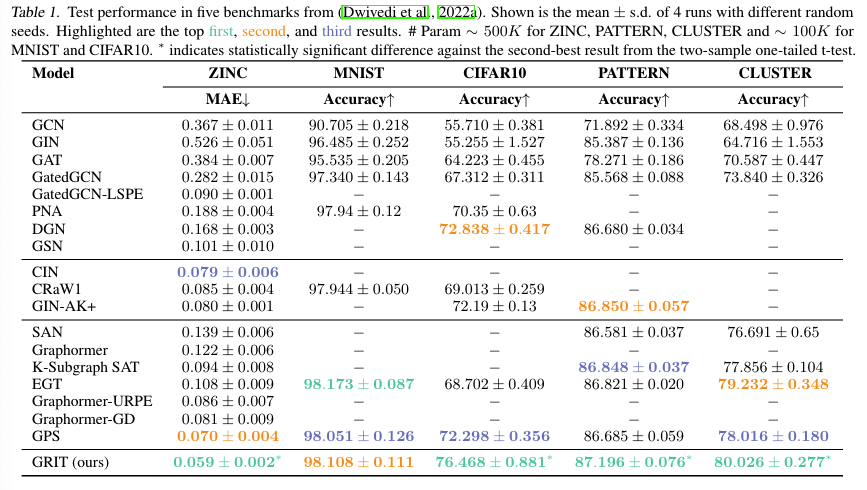
2.7.1.1 Benchmarks from Benchmarking GNNs
- Datasets:
- ZINC
- MNIST
- CIFAR 10
- PATTERN
- CLUSTER
- Metrics:
- MAE
- Accuracy
- Accuracy
- Accuracy
- Accuracy
- Baselines:
- MPNNs
- GCN
- GIN
- GAT
- GatedGCN
- GatedGCN-LSPE
- PNA
- DGN
- GSN
- Other recent GNNs with SOTA performance
- CIN
- CRaW1
- GIN-AK+
- Graph Transformers
- SAN
- Graphormer
- K-Subgraph SAT
- EGT
- Graphormer-URPE
- Graphformer-GD,
- Hybrid Graph Transformer
- GPS
- MPNNs
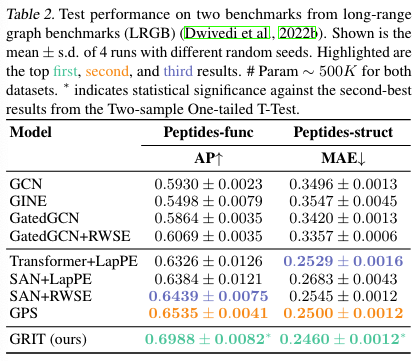
2.7.1.2 Long-Range Graph Benchmark
- Datasets
- Baselines
- Metrics
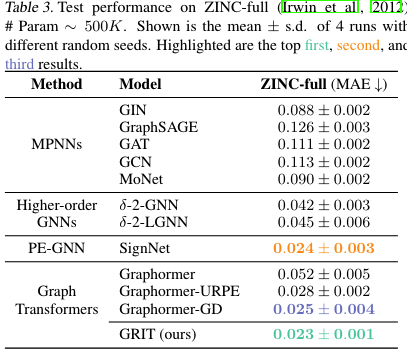
2.7.1.3 ZINC-full Dataset
- Datasets
- Baselines
- Metrics
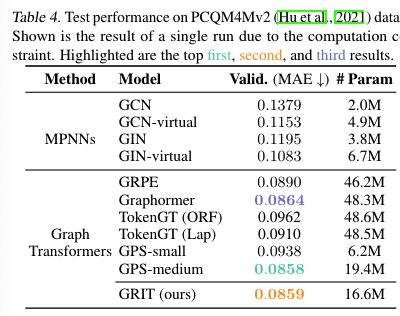
2.7.1.4 PCQM4Mv2 Large-scale Graph Regression Benchmark
- Datasets
- Baselines
- Metrics
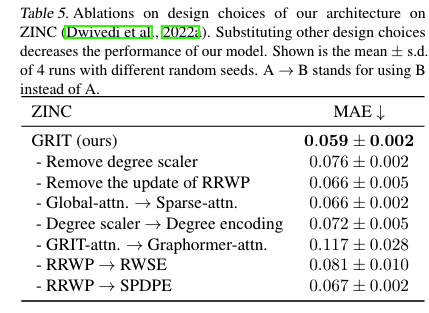
2.7.2 Ablations
- Datasets
- Variants
- Metrics
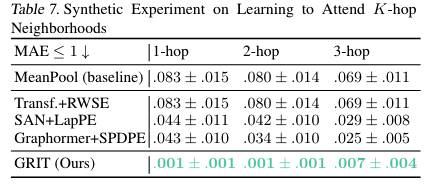
2.7.3 Synthetic Experiment
- Datasets
- Parameters to analyse
- Metrics
2.8 论文中的实验及结果有没有很好地支持需要验证的科学假设?
2.8.1 Benchmarking GRIT
[!Summary] Benchmarks from Benchmarking GNNs
实验:结果:
结论:
[!Summary] Long-Range Graph Benchmark
实验:结果:
结论:
[!Summary] ZINC-full Dataset
实验:结果:
结论:
[!Summary] PCQM4Mv2 Large-scale Graph Regression Benchmark
实验:结果:
结论:
2.8.2 Ablations
[!Summary] Ablations
实验:结果:
结论:
2.8.3 Synthetic Experiment
[!Summary] Synthetic Experiment
实验:
结果:
结论:
2.9 这篇论文到底有什么贡献?
- Arguing for the importance of graph inductive biases in Graph Transformers.
2.10 下一步呢?有什么工作可以继续深入?
- Computational complexity
- Upper bounds on expressive power